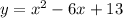HELP PLZ!! Which equation represents a parabola that opens upward, has a minimum at x = 3, and has a line of symmetry at x = 3? A. y = x^2 - 3x + 6\\\\B. y = x^2 + 8x + 19\\\\C.…

Question

HELP PLZ!!

Which equation represents a parabola that opens upward, has a minimum at x = 3, and has a line of symmetry at x = 3?


`A. y = x^2 - 3x + 6\\\\B. y = x^2 + 8x + 19\\\\C. y = x^2 + 6x + 5\\\\D. y = x^2 - 6x + 13`

Answer 1

D. y = x^2 -6x + 13

Explanation:

Answer 2

`y=x^2-6x+13`

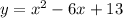
Explanation:

All the parabolas open upwards because they all have an 'a' value of a=1 which is positive.

The axis of symmetry of a parabola is calculated using the formula;

`x=-(b)/(2a)`

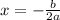
We have x=3 and a=1.

We substitute the values to get;

`3=-(b)/(2(1))`

`-2* 3=-(b)/(2)* -2`

`b=-6`

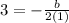
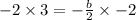
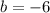
Therefore the equation is of the form;

`y=x^2-6x+c`

Looking at the given options, the required equation is

`y=x^2-6x+13`