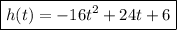Answer:
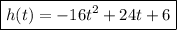
Step-by-step explanation:
From the statement of the problem we know:
The graph shows the height (h), in feet, of a basketball t seconds after it is shot. Projectile motion formula:
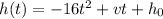
 = initial vertical velocity of the ball in feet per second
= initial vertical velocity of the ball in feet per second
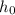 = initial height of the ball in feet Complete the quadratic equation that models the situation.
= initial height of the ball in feet Complete the quadratic equation that models the situation.
From the graph we know:
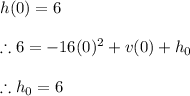
For a quadratic function:
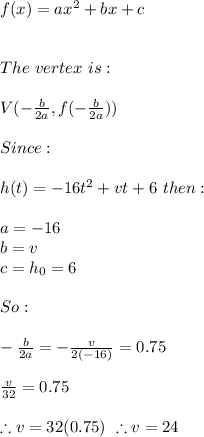
Finally: