For this case we must simplify the following expression:

By definition of properties of powers and roots, we have to:
![\sqrt [n] {a ^ m} = a ^ {\frac {m} {n}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/suo6ai2uezolc3t7f2f9e9h1lijquf271f.png)
Then, rewriting the expression:
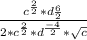

By definition of properties of division of powers of equal base we have to;
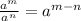
Rewriting the expression:
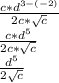
Answer:
Option B