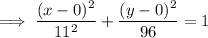Answer:
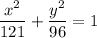
Explanation:
General equation of an ellipse:
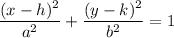
where:
- center = (h, k)
- Vertices = (h±a, k) and (h, k±b)
- Foci = (h±c, k) and (k, h±c) where c²=a²−b²
- Major Axis: longest diameter of an ellipse
- Minor Axis: shortest diameter of an ellipse
- Major radius: one half of the major axis
- Minor radius: one half of the minor axis
If a > b the ellipse is horizontal, a is the major radius, and b is the minor radius.
If b > a the ellipse is vertical, b is the major radius, and a is the minor radius.
Given:
- foci = (-5, 0) and (5, 0)
- vertices = (-11, 0) and (11, 0)
Therefore, the ellipse is horizontal with its center at (0, 0):
⇒ h = 0 and k = 0
⇒ a = 11
⇒ c = 5
To find b², use c² = a² − b²:
⇒ 5² = 11² − b²
⇒ b² = 11² − 5²
⇒ b² = 96
Therefore, the standard form of the equation of the ellipse is: