Answer:
Part 1)
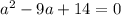 -----> solution set {7,2}
-----> solution set {7,2}
Part 2)
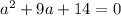 -----> solution set {-2,-7}
-----> solution set {-2,-7}
Part 3)
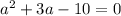 -----> solution set {2,-5}
-----> solution set {2,-5}
Part 4)
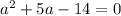 ----> solution set {2,-7}
----> solution set {2,-7}
Part 5)
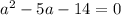 ----> solution set {-2,7}
----> solution set {-2,7}
Explanation:
we know that
The formula to solve a quadratic equation of the form
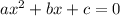
is equal to
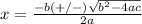
Part 1)
in this problem we have
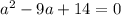
so
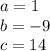
substitute in the formula
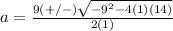
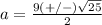
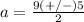
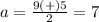
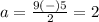
The solution set is {7,2}
Part 2)
in this problem we have
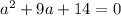
so
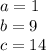
substitute in the formula
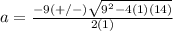
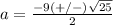
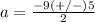
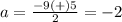
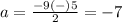
The solution set is {-2,-7}
Part 3)
in this problem we have
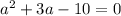
so
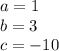
substitute in the formula
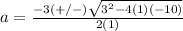
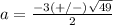
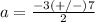
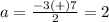
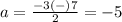
The solution set is {2,-5}
Part 4)
in this problem we have
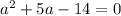
so
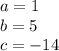
substitute in the formula
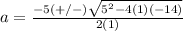
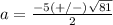
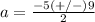
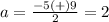
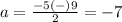
The solution set is {2,-7}
Part 5)
in this problem we have
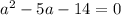
so
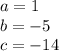
substitute in the formula
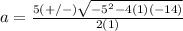
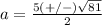
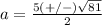
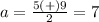
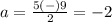
The solution set is {-2,7}