Question

This is about three variable systems but i can’t figure out how to solve it.

Answer 1

The chemist combines
`x` L of solution A,
`y` of solution B, and
`z` of solution C to get a 60 L solution, which means

`x+y+z=60`

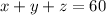
The chemist used twice as much of solution C as solution A, so

`z=2x`

This mixture contains 29% acid, which means 29% of the total 60 L, or 17.4 L, is acid. For every liter of solution A, there are 0.15 L of acid. Similarly, every liter of solution B contributes 0.05 L of acid, and solution C contributes 0.40 L. This means we have

`0.15x+0.05y+0.40z=17.4`

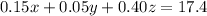
So the system you have to solve is

`\begin{cases}x+y+z=60\\0.15x+0.05y+0.4z=17.4\\z=2x\end{cases}`

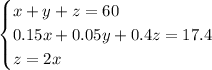
Substitute
`z=2x` into the first two equations:

`\begin{cases}x+y+2x=60\\0.15x+0.05y+0.4(2x)=17.4\end{cases}\implies\begin{cases}3x+y=60\\0.95x+0.05y=17.4\end{cases}`

Write the first equation as

`3x+y=60\implies y=60-3x`

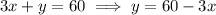
and substitute this into the other equation:

`0.95x+0.05(60-3x)=17.4\implies0.8x+3=17.4\implies0.8x=14.4\implies x=18`

We can solve for
`z` at this point:

`z=2x\implies z=36`

Then solve for
`y`:

`y=60-3x\implies y=6`

So the chemist used 18 L of solution A, 6 L of solution B, and 36 L of solution C.