Question

what two- dimensional shape is formed by a cross section of the cube shown if the cross section passes through the midpoints of three edges that intersect at the same vertics of the cube A= scalene triangle B= square C= equilateral triangle D = rectangle

Answer 1

C= equilateral triangle

Explanation:

To find this answer we need to know what a cube is. A cube is a prism whose sides all have the same length. It's something like the three dimensional version of a square. In the figure below, we have labeled each length of the cube as
`x`. Also, the vertex we taken is in blue color, so we need to find each side length of the triangle. Since the cross section passes through the midpoints of three edges that intersect at the same vertices of the cube, then:

`L_(1)=\sqrt{((x)/(2))^2+((x)/(2))^2} \\ \\ L_(1)=\sqrt{(x^2)/(4)+(x^2)/(4)} \\ \\ L_(1)=\sqrt{(2x^2)/(4)} \\ \\ L_(1)=\sqrt{(x^2)/(2)} \\ \\ L_(1)=(x)/(√(2)) \\ \\ L_(1)=(x)/(√(2))(√(2))/(√(2)) \\ \\ L_(1)=(√(2)x)/(2)`

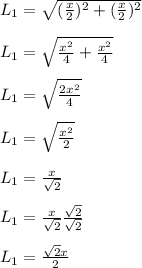
Since this is a cube, then it is true that:

`L_(1)=L_(2)=L_(3)=(√(2)x)/(2)`

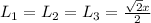
Since the side lengths have the same value, this is an equilateral triangle.