Question

Determine the equations of the vertical and horizontal asymptotes if any for h(x)=(x+1)^2/x^2-1

Answer 1

x=1

y=1

Explanation:

C on edge!

Answer 2

Vertical asymptote:

x=1

Horizontal asymptote:

y=1

EXPLANATION

The given rational function is

`h(x) = \frac{ {(x + 1)}^(2) }{ {x}^(2) - 1 }`

`h(x) = \frac{ {(x + 1)}^(2) }{ ({x} - 1)(x + 1)}`

`h(x) = \frac{ (x + 1)(x + 1) }{ ({x} - 1)(x + 1)}`

`h(x) = \frac{ x + 1}{ {x} - 1}`

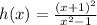
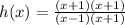
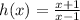
The vertical asymptote occurs at

`{x} - 1 = 0`

`x = 1`

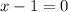
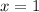
The vertical asymptotes is x=1

The degree of the numerator is the same as the degree of the denominator.

The horizontal asymptote of such rational function is found by expressing the coefficient of the leading term in the numerator over that of the denominator.

`y = (1)/(1)`

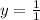
y=1