Question

Y = 4x+1 y=x^2 + 2x - 2 A.6,2 B. 2,6 C. -6,2 D. -6,-2

Answer 1

The solution is (3,13) and (-1,-3). So none of the mentioned options is correct.

Explanation:

Given that

`y = 4x + 1  (i)`

`y = x^2 + 2x -2 (ii)`

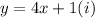
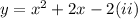
Now, by susbstituting the value of 'y' from equation i to equation ii, we get

`4x+1=x^2 + 2x -2`

`0=x^2 + 2x -2-4x-1`

`0=x^2 + (2x -4x) +(-2-1)`

`0=x^2 + (-2x) +(-3)`

`0=x^2 -2x -3`

`x^2 -2x -3 = 0 (iii)`

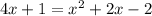
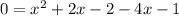
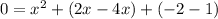
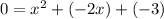
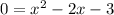
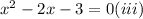
Now by factorization, equation iii can be written as

`x^2 -3x +x -3 = 0`

`x(x -3) + 1(x -3) = 0`

`(x -3)(x +1) = 0`

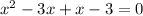
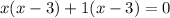
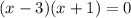
x = 3 and x = -1

By putting the values of x in equation i, we get

y = 4(3) + 1

y = 12 +1

y = 13

and

y = 4(-1) + 1

y = -4 +1

y = -3

Therefore, the solution is (3,13) and (-1,-3). So none of the mentioned options is correct.