Question

Find the vertices and foci of the hyperbola with equation quantity x plus 5 squared divided by 36 minus the quantity of y plus 1 squared divided by 64 equals 1.

Vertices: (-1, 3), (-1, -13); Foci: (-1, -13), (-1, 3)
Vertices: (3, -1), (-13, -1); Foci: (-13, -1), (3, -1)
Vertices: (-1, 1), (-1, -11); Foci: (-1, -15), (-1, 5)
Vertices: (1, -1), (-11, -1); Foci: (-15, -1), (5, -1)

Answer 1

Vertices: (1,-1), (-11, -1); Foci: (-15, -1), (5, -1)

Explanation:

Center at (-5,-1) because of the plus 5 added to the x and the plus 1 added to the y.

a(squared)=36 which means a=6 and a=distance from center to vertices so add and subtract 6 from the x coordinate since this is a horizontal hyperbola, which is (1,-1), (-11,-1). From there you dont need to find the focus since there is only one option for this;

Vertices: (1,-1), (-11, -1); Foci: (-15, -1), (5, -1)

Answer 2

Vertices: (1, -1), (-11, -1); Foci: (-15, -1), (5, -1)

Explanation:

Ok so we have 5x
`(5x^(2) )/(36)-(y^(2) )/(64)=1`

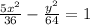
As you know we have the equation of the hyperbola as (x-h)^2/a^2-(y-k)^2/b^2, so the formula of the foci is
`(h+-c,k) and for vertices (h+-a,k)`

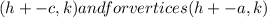
then we have to calculate c using pythagoras theorem we have that

a=6 because is the root of 36

b=8 beacause is the root of 64

And then we have that
`c^(2)=a^(2)+b^(2)`

`c=√(36+64)`

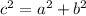
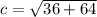
So the root of 100 is equal to 10

Hence c=10

Using the formula given before and the equation we know that

h=-5

k=-1

And replacing those values on the equation we have that the foci are

• (-5-10, -1)=(-15,-1)

• (-5+10,1)=(5,-1)

And the vertices are:

• (-5-6, -1)=(-11,-1)
• (-5+6, 1)= (1,-1)

So the correct answer is D