Question

The points (4, 1) and (x, -6) lie on the same line. If the slope of the line is 1 what is the value of x?

Answer 1

The value of x is -3

Explanation:

* Lets explain how to solve the problem

- The slope of a line that passes through points (x1 , y1) and (x2 , y2) is

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

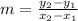
* Lets solve the problem

∵ The points (4 , 1) and (x , -6) lie on the same line

∵ The slope of the line is 1

- Let the point (4 , 1) is (x1 , y1) and the point (x , -6) ix (x2 , y2)

∵ x1 = 4 , x2 = x and y1 = 1 , y2 = -6

∴
`m=(x-4)/(-6-1)`

∴
`m=(x-4)/(-7)`

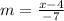
∵ The slope of the line is m = 1

∴
`(x-4)/(-7)=1`

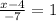
- By using cross multiplication

∴ x - 4 = -7 ⇒ add 4 to both sides

∴ x = -3

* The value of x is -3