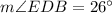Answer:
B.
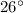
Explanation:
We are given that a triangle ABD, BE is perpendicular to AD and angle EBD is congruent to angle CBD.
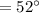
We have to find the measure of angle EDB.
Let
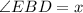
Then,
 because angle EBD is congruent to angle CBD.
because angle EBD is congruent to angle CBD.
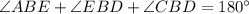 (linear sum)
(linear sum)
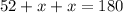
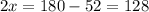
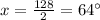
In triangle EBD
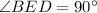
![\angle EBD=64^{\circ]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/n2921p6z0ja60fkfbwyx78qeq5clfue95v.png)
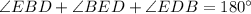 (sum of angles of triangle )
(sum of angles of triangle )
Substitute the values then we get
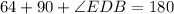
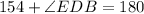
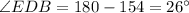
Hence,