Question

What is the measure of ∠JSM?
A) 12°
B) 17°
C) 23°
D) 31°

Answer 1

I think it would be “B”

Answer 2

Option B.

Explanation:

Given information:
`m\angle A=48^(\circ),\angle E=90^(\circ),\angle EMS=59^(\circ)`.

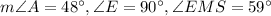According to the angle sum property of a triangles, the sum of interior angles of a triangle is 180°.

Apply angle sum property on triangle AEJ.

`\angle A+\angle E+\angle J=180^(\circ)`

`48^(\circ)+90^(\circ)+\angle J=180^(\circ)`

`138^(\circ)+\angle J=180^(\circ)`

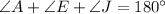
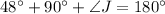
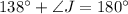
Subtract 138 from both sides.

`\angle J=180^(\circ)-138^(\circ)`

`\angle J=42^(\circ)`

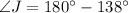
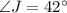
The measure of angle J is 42°.

According to exterior angle property, the sum of two interior angles of a triangle is equal to the third exterior angle.

Apply exterior angle property on triangle JMS.

`\angle EJA+\angle JSM=\angle EMS`

`42^(\circ)+\angle JSM=59^(\circ)`

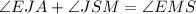
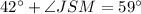
Subtract 42 from both sides.

`\angle JSM=59^(\circ)-42^(\circ)`

`\angle JSM=17^(\circ)`

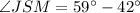
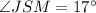
The measure of ∠JSM is 17°.

Therefore, the correct option is B.