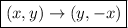Answer:
Transformations are important subjects in geometry. In this exercise, these are the correct transformation rules:
1. Reflection over x-axis:
Consider the point
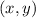 , if you reflect this point across the x-axis you should multiply the y-coordinate by -1, so you get:
, if you reflect this point across the x-axis you should multiply the y-coordinate by -1, so you get:
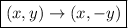
2. Reflection over y-axis:
Consider the point
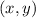 , if you reflect this point across the y-axis you should multiply the x-coordinate by -1, so you get:
, if you reflect this point across the y-axis you should multiply the x-coordinate by -1, so you get:
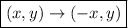
3. Rotation of 90° counter-clockwise about origin:
Consider the point
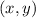 . To rotate this point by 90° around the origin in counterclockwise direction, you can always swap the x- and y-coordinates and then multiply the new x-coordinate by -1. In a mathematical language this is as follows:
. To rotate this point by 90° around the origin in counterclockwise direction, you can always swap the x- and y-coordinates and then multiply the new x-coordinate by -1. In a mathematical language this is as follows:
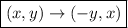
4. Rotation of 180° counter-clockwise about origin:
Consider the point
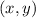 . To rotate this point by 180° around the origin, you can flip the sign of both the x- and y-coordinates. In a mathematical language this is as follows:
. To rotate this point by 180° around the origin, you can flip the sign of both the x- and y-coordinates. In a mathematical language this is as follows:
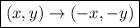
5. Rotation of 270° counter-clockwise about origin:
Rotate a point 270° counter-clockwise about origin is the same as rotating the point 90° in clock-wise direction. So the rule is: