Question

Create triangle A’B’C by reflecting triangle ABC over the y-axis on the coordinate plane. What are the new coordinates of the vertices?

Answer 1

Explanation:

When talking about reflection, we usually mean reflecting across a line, or axis. Reflecting a shape means looking at the mirror image on the other side of the axis. Consider the point (x,y), if you reflect this point across the y-axis you should multiply the x-coordinate by -1, so you get:

`(x,y)\rightarrow(-x,y)`

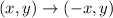
For triangle ABC we have:

`A(-4,2) \\ \\ B(-1,3) \\ \\ C(-1,-4)`

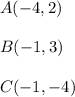
Therefore, the reflecting points are:

`A'(4,2) \\ \\ B(1,3) \\ \\ C(1,-4)`

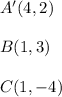
Both the original triangle and the reflected one are shown below.