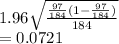Question

In a random sample of 184 college students, 97 had part-time jobs. Find the margin of error for the 95% confidence interval used to estimate the population proportion. 0.0649

0.1260

0.0721

0.0027

Answer 1

0.0721

That’s your answer

Answer 2

0.0721

Explanation:

A 95% confidence interval for the population proportion is calculated using the formula;

`p+/-1.96\sqrt{(p(1-p))/(n) }`

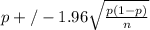
In this case p is the sample proportion, calculated as ;

number of successes/sample size. It is the equivalent of the probability of success in a binomial distribution. This implies that the sample proportion in this case will be; 97/184

The value 1.96 is the confidence coefficient associated with a 95% confidence interval for the population proportion since the sample proportions under the central limit theorem are assumed o be normally distributed.

n is simply the sample size, 184 college students.

Now, the expression

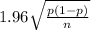`1.96\sqrt{(p(1-p))/(n) }` is what is termed as the margin of error for a 95% confidence interval of the population proportion. We simply substitute the values given into the expression and simplify it.

`1.96\sqrt{((97)/(184) (1-(97)/(184) ))/(184) }\\ =0.0721`