The limit is (famously)
 by definition, but if you want to compute it via L'Hopital's rule:
by definition, but if you want to compute it via L'Hopital's rule:
![\displaystyle\lim_(x\to\infty)\left(1+\frac1x\right)^x=\lim_(x\to\infty)\exp\left(\ln\left(1+\frac1x\right)^x\right)=\exp\left(\lim_(x\to\infty)x\ln\left(1+\frac 1x\right)\right)=\exp\left(\lim_(x\to\infty)(\ln\left(1+\frac1x\right))/(\frac1x)\right)]()
where
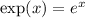 . As
. As
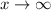 , the numerator approaches
, the numerator approaches
 and the denominator approaches 0. Applying L'Hopital's rule gives
and the denominator approaches 0. Applying L'Hopital's rule gives

The remaining approaches 1, so the original limit is
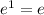 , as expected.
, as expected.