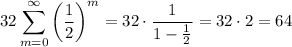You can factor the 32 out of the sum:
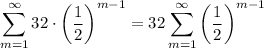
We can also change the index as follows
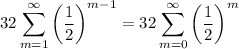
Now, we have a theorem that states that the series
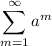
converges if and only if
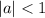 , and in this case we have
, and in this case we have
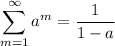
This is your case, because you have
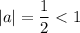
which implies that your series converges, and the value is