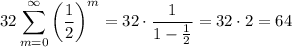Question

Please help me solve this​

Answer 1

You can factor the 32 out of the sum:

`\displaystyle \sum_(m=1)^\infty 32 \cdot \left((1)/(2)\right)^(m-1) = 32\sum_(m=1)^\infty \left((1)/(2)\right)^(m-1)`

We can also change the index as follows

`\displaystyle 32\sum_(m=1)^\infty \left((1)/(2)\right)^(m-1) = 32\sum_(m=0)^\infty \left((1)/(2)\right)^(m)`

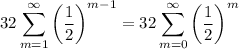
Now, we have a theorem that states that the series

`\displaystyle \sum_(m=1)^\infty a^m`

converges if and only if
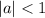`|a|<1`, and in this case we have

`\displaystyle \sum_(m=1)^\infty a^m = (1)/(1-a)`

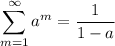
This is your case, because you have

`|a|=(1)/(2)<1`

which implies that your series converges, and the value is

`\displaystyle 32\sum_(m=0)^\infty \left((1)/(2)\right)^(m) = 32 \cdot (1)/(1-(1)/(2)) = 32\cdot 2 = 64`