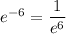De l'Hospital rule applies to undetermined forms like
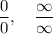
If we evaluate your limit directly, we have
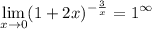
which is neither of the two forms covered by the theorem.
So, in order to apply it, we need to write the limit as follows: we start with
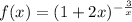
Using the identity
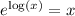 , we can rewrite the function as
, we can rewrite the function as
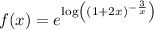
Using the rule
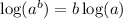 , we have
, we have
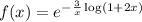
Since the exponential function
 is continuous, we have
is continuous, we have

In other words, we can focus on the exponent alone to solve the limit. So, we're focusing on
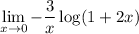
Which we can rewrite as
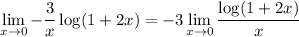
Now the limit comes in the form 0/0, so we can apply the theorem: we derive both numerator and denominator to get

So, the limit of the exponent is -6, which implies that the whole expression tends to