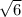Question

What is the center and radius for the circle with equation 2x^2-8x+2y^2+12y+14=0​

Answer 1

Center : (2,-3)

Radius : sqrt(6)

Explanation:

Rewrite this is standard form to find the center and radius.

(x-2)^2 + (y+3)^2 = 6

From this, we can determine that the center is (2,-3) and the radius is sqrt(6)

Answer 2

center is (2,-3)

Radius =
`√(6)`

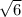
Explanation:

`2x^2-8x+2y^2+12y+14=0`

To find out the center and radius we write the given equation in

(x-h)^2 +(y-k)^2 = r^2 form

Apply completing the square method

`2x^2-8x+2y^2+12y+14=0`

`(2x^2-8x)+(2y^2+12y)+14=0`

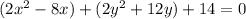
factor out 2 from each group

`2(x^2-4x)+2(y^2+6y)+14=0`

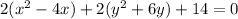
Take half of coefficient of middle term of each group and square it

add and subtract the numbers

4/2= 2, 2^2 = 4

6/2= 3, 3^2 = 9

`2(x^2-4x+4-4)+2(y^2+6y+9-9)+14=0`

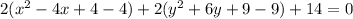
now multiply -4 and -9 with 2 to take out from parenthesis

`2(x^2-4x+4)+2(y^2+6y+9)+14-8-18=0`

`2(x-2)^2 +2(y+3)^2 -12=0`

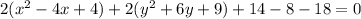
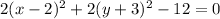
Divide whole equation by 2

`(x-2)^2 +(y+3)^2 -6=0`

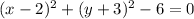
Add 6 on both sides

`(x-2)^2 +(y+3)^2 -6=0`

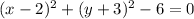
now compare with equation

(x-h)^2 + (y-k)^2 = r^2

center is (h,k) and radius is r

center is (2,-3)

r^2 = 6

Radius =
`√(6)`