Answer: The correct option is
(D) a clockwise rotation of 90° about the origin then a translation of 2 units right and 4 units up.
Step-by-step explanation: We are given to select the series of transformations that map triangle ABC into triangle DEF to prove that ΔABC ≅ ΔDEF.
From the graph, we note that
the co-ordinates of the vertices of ΔABC are A(0, 3), B(-2, 6) and C(2, 6).
And,
the co-ordinates of the vertices of triangle ΔDEF are D(5, 4), E(8, 6) and C(8, 2).
We know that
if a point (x, y) is rotated 90° clockwise, its co-ordinates becomes (y, -x). Also, if we translate a point 2 units to the right and 4 units up, then the final co-ordinates of the point (x, y) will be
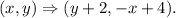
So, if triangle ABC is rotated 90° clockwise, translated 2 units right and 4 units up, then the co-ordinates of the vertices becomes
A(0, 3) ⇒ (3+2, -0+4) = (5, 4),
B(-2, 6) ⇒ (6+2, 2+4) = (8, 6)
and
C(2, 6) ⇒ (6+2, -2+4) = (8, 2).
We see that the new co-ordinates are the co-ordinates of the vertices of triangle DEF, i.e., D(5, 4), E(8, 6) and C(8, 2).
Thus, the required series of transformations that map ΔABC into ΔDEF are
a clockwise rotation of 90° about the origin then a translation of 2 units right and 4 units up.
Option (D) is CORRECT.