Question

Suppose that $12,724 is invested at an interest rate of 6.1% per year, compounded continuously. Find the exponential function that describes the amount in the account after time t, in years. What is the balance after 1 year, 2 years, 5 years, 10 years. What is the doubling time

Answer 1

Exponential Function:
`A= P* e ^ {0.061t}`

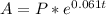
Balance after

t=1 $ 13,524.32

t=2 $ 14,374.99

t=5 $ 17,261.69

t=10 $ 23,417.64

Explanation:

Formula used to find amount in the account after time t, given the interest rate is compounded continuously

`A= Pe^r^t`

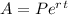
where: P= principal amount or amount invested

r= interest rate

t= time

A= amount after time t

in our question we are given:

P=$12,724

r= 6.1% or 0.061

`A= 12724 * e ^ (^0^.^0^6^1^)^t`

The above equation is exponential function that describes the amount in the account after time t in years

Now, for t = 1

`A= 12724 * e ^ {0.061 * 1}`

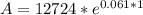
A= $ 13,524.32

t=2

`A= 12724 * e ^ {0.061 * 2}`

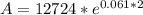
A= $ 14,374.99

t= 5

`A= 12724 * e ^ {0.061 * 5}`

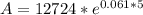
A= $ 17,261.69

t=10

`A= 12724 * e ^ {0.061 * 10}`

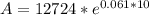
A= $ 23,417.64