Question

1. A baseball is thrown into the air with an upward velocity of 25 ft/sec. It’s height (in feet) after t seconds can be modeled by the function h(t) = -16t^2 + 25t + 5. Algebraically determine how long will it take the ball to reach its maximum height? What is the ball’s maximum height?

2. A company that sells digital cameras has found that their revenue can be remodeled by the equation R(p) = -5p^2 + 1230p, where p is the price of the camera in dollars. Algebraically determine what price will maximize the revenue? What is the maximum revenue?

Answer 1

1. Algebraically determine how long will it take the ball to reach its maximum height? What is the ball’s maximum height?

We can use the concept of derivative to find this result, but since the problem states we must use algebraic procedures, then we solve this as follows:

• Step 1: Write the original equation:

`h(t)=-16t^2+25t+5`

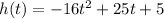
• Step 2: Common factor -16:

`h(t)=-16(t^2-(25)/(16)t-(5)/(16))`

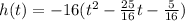
• Step 3: Take half of the x-term coefficient and square it. Add and subtract this value:

X-term:
`-(25)/(16)`

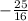
Half of the x term:
`-(25)/(32)`

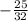
After squaring:
`(-(25)/(32))^2=(625)/(1024)`

`h(t)=-16(t^2-(25)/(16)t-(5)/(16)+(625)/(1024)-(625)/(1024)) \\ \\ h(t)=-16(t^2-(25)/(16)t+(625)/(1024)-(5)/(16)-(625)/(1024)) \\ \\ h(t)=-16(t^2-(25)/(16)t+(625)/(1024)-(945)/(1024)) \\ \\`

• Step 4: Write the perfect square:

`h(t)=-16[(t-(25)/(32))^2-(945)/(1024)] \\ \\ \boxed{h(t)=-16(t-(25)/(32))^2-(945)/(64)}`

Finally, the vertex of this function is:

`((25)/(32),(945)/(64))`

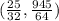
So in this vertex we can find the answer to this problem:

The ball will reach its maximum height at
`t=(25)/(32)s=0.78s`

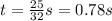
The ball maximum height is
`H=(945)/(64)=14.76ft`

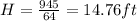
2. Algebraically determine what price will maximize the revenue? What is the maximum revenue?

Also we will use completing squares. We can use the concept of derivative to find this result, but since the problem states we must use algebraic procedures, then we solve this as follows:

• Step 1: Write the original equation:

`R(p)=-5p^2+1230p`

• Step 2: Common factor -5:

`R(p)=-5(p^2-246p)`

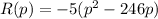
• Step 3: Take half of the x-term coefficient and square it. Add and subtract this value:

X-term:
`-246`

Half of the x term:
`-123`

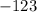
After squaring:
`(-123)^2=15129`

`R(p)=-5(p^2-246p+15129-15129)`

• Step 4: Write the perfect square:

`R(p)=-5[(x-123p)^2-15129] \\ \\ R(p)=-5(x-123p)^2+75645`

Finally, the vertex of this function is:

`(123,75645)`

So in this vertex we can find the answer to this problem:

The price will maximize the revenue is
`p=123 \ dollars`

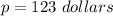
The maximum revenue is
`R=75645`