Question

Newton's Law of Cooling states that the rate of change of the temperature of an object, T, is proportional to the difference of T and the temperature of the region, TR or dT over dt equals k times the quantity T minus T sub R end quantity. An object with core temperature of 1200°F is removed from a fire and placed in a region with a constant temperature of 80°F. After 1 hour, its core temperature is 830°F. What is the object's core temperature 4 hours after it is taken off the fire? (1 point)

Answer 1

305 °F

Explanation:

The core temperature of the object after 4 hours can be found using an exponential decay formula to model the decay of the difference between core temperature and ambient.

Cooling Model

The solution to the differential equation described by Newton's law of cooling is the exponential equation ...

y = ab^t +c

where 'a' is the initial core temperature difference from ambient, 'b' is the decay factor of that difference in 1 unit of time period t. 'c' is the ambient temperature.

For this problem, the ambient temperature is c=80, and the differences of interest are ...

a = 1200 -80 = 1120

b = (830 -80)/1120 = 75/112

Using these values in the model gives ...

y = 1120(75/112)^t +80 . . . . . . where y(t) is the core temperature at time t

Note that units of time are hours.

Application

We want y when t=4.

y = 1120(75/112)^4 +80 ≈ 1120(0.20108) +80 ≈ 305.212

The core temperature after 4 hours is about 305 °F.

__

Additional comment

The differential equation will have a solution of the form ...

`T-T_R=(T_0-T_R)e^(kt)`

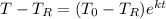
where k = ln(75/112) ≈ -0.40101

In the above, we defined b = e^k = 75/112. Accuracy with this fraction can be better than using a truncated value of k.