Answer:
305 °F
Explanation:
The core temperature of the object after 4 hours can be found using an exponential decay formula to model the decay of the difference between core temperature and ambient.
Cooling Model
The solution to the differential equation described by Newton's law of cooling is the exponential equation ...
y = ab^t +c
where 'a' is the initial core temperature difference from ambient, 'b' is the decay factor of that difference in 1 unit of time period t. 'c' is the ambient temperature.
For this problem, the ambient temperature is c=80, and the differences of interest are ...
a = 1200 -80 = 1120
b = (830 -80)/1120 = 75/112
Using these values in the model gives ...
y = 1120(75/112)^t +80 . . . . . . where y(t) is the core temperature at time t
Note that units of time are hours.
Application
We want y when t=4.
y = 1120(75/112)^4 +80 ≈ 1120(0.20108) +80 ≈ 305.212
The core temperature after 4 hours is about 305 °F.
__
Additional comment
The differential equation will have a solution of the form ...
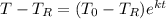
where k = ln(75/112) ≈ -0.40101
In the above, we defined b = e^k = 75/112. Accuracy with this fraction can be better than using a truncated value of k.