Answer: Option a.
Domain: (-∞, ∞)
Range: (-∞, ∞)
Explanation:
We have the function
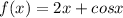
Note that f(x) is the sum of two continuous functions
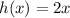 and
and
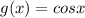
The domain and range of h(x) are all real numbers
The domain of g(x) is all real numbers. The range of g(x) is [-1, 1]
Then the domain of
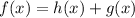 will be the intersection of the domains of the function
will be the intersection of the domains of the function
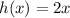 and the function
and the function
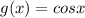 .
.
Therefore the domain of f(x) are all real numbers. x ∈ (-∞, ∞)
The range of f(x) will be equal to the union of the range of g(x) and h(x)
Therefore the range will be all real numbers f(x) ∈ (-∞, ∞)