Question

Fine the maximum and minimum values of the function y= -cos8x

Answer 1

`\boxed{ \text{Min. = -1; max. = 1}}\\`

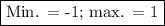
Explanation:

The value of cosx ranges from -1 to 1, so -cosx ranges from 1 to -1.

The minimum value is -1, and the maximum value is +1.

`\boxed{ \textbf{Min. = -1; max. = 1}}\\`

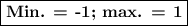
The number 8 in the argument does not affect the amplitude of the wave. It affects only the frequency.

In the diagram, both y = -cos8x (purple) and y = -cosx (black) range from -1 to +1, but the purple cosine curve has eight times the frequency of the black one.