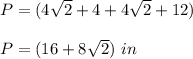2 Answers

Silly John · Answer 1 · 2020-11-08T02:14:50+0000

Answer:

The perimeter of one of the trapezoids is equal to
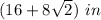
$(16+8√(2))\ in$

Explanation:

see the attached figure to better understand the problem

we know that

The perimeter of a square is

P=4b

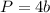
where

b is the length side of the square

step 1

Find the length side of the smaller square

16=4b

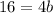
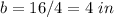
$b=16/4=4\ in$

step 2

Find the length side of the large square

48=4b

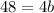
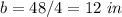
$b=48/4=12\ in$

step 3

Find the height of one trapezoid

The height is equal to

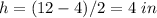
$h=(12-4)/2=4\ in$

step 4

Remember that in this problem, one trapezoid is equal to one square plus two isosceles right triangles.

Find the hypotenuse of one isosceles right triangle

Applying Pythagoras Theorem

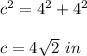
$c^(2)=4^(2) +4^(2) \\ \\c=4√(2)\ in$

step 5

Find the perimeter of one of the trapezoid

The perimeter is equal to

$P=(4√(2) +4+4√(2)+12)\\ \\P=(16+8√(2))\ in$

Please log in or register to add a comment.