Question

Which statement is true about the distribution?

A. Either the IQR or the range are good measures of variability because the distribution has an outlier

B. the IQR is the best measure of variability because the distribution has not outliers.

C. Either the IQR or the range are good measures of variability because the distribution has no outliers

D. The range is the best measure of variability because the distribution has an outlier

Answer 1

it would be C. Either the IQR or the range are good measures of variability because the distribution has no outliers

Explanation:

Answer 2

Answer with explanation:

Lowest Variate in distribution =10

Largest Variate in distribution =45

Range =Maximum Variate - Minimum Variate

= 45 -10

=35

→First Quartile

`Q_(1)=15`

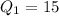
→Median =Q= 25

→Third Quartile

`Q_(3)=40`

IQR=Inter Quartile Range

`=Q_(3)-Q_(1)\\\\=40-15\\\\=25`

To calculate Outliers

`\rightarrow Q_(3) + 1.5* IQR=40 +1.5 * 25\\\\=40 +3.75\\\\=43.75\\\\\rightarrow Q_(1) - 1.5* IQR\\\\=15 - 1.5 * 25\\\\=15 - 3.75\\\\=11.25`

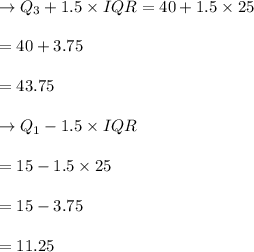
→Numbers below, 11.25 and numbers above 43.75 are outliers.

So, both , 10 and 45 , are outliers.

Therefore, range is not good measure of variability.

→→I QR , is better measure of Variability.

But , Option A,⇒ Either the IQR or the range are good measures of variability because the distribution has an outlier.