Question

The photon energies used in different types of medical x-ray imaging vary widely, depending upon the application. Single dental x rays use photons with energies of about 25 keV. The energies used for x-ray microtomography, a process that allows repeated imaging in single planes at varying depths within the sample, is 2.5 times greater.

What are the wavelengths of the x rays used for these two purposes?

Answer 1

1. Single dental x-rays:
`5.0\cdot 10^(-11)m`

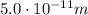
The energy of the photon is

`E=25 keV = 25,000 eV`

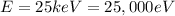
Using the conversion factor

`1 eV=1.6\cdot 10^(-19) J`

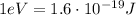
we can convert it into Joules:

`E=(25,000 eV)(1.6\cdot 10^(-19)J/eV)=4\cdot 10^(-15) J`

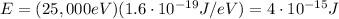
The relationship between photon energy and wavelength is

`\lambda=(hc)/(E)`

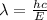
where

`h=6.63\cdot 10^(-34) Js` is the Planck constant

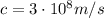`c=3\cdot 10^8 m/s` is the speed of light

E is the energy

Substituting into the formula, we find

`\lambda=((6.63\cdot 10^(-34)Js)(3\cdot 10^8 m/s))/(4\cdot 10^(-15) J)=5.0\cdot 10^(-11)m`

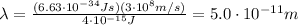
2. Microtomography:
`2.0\cdot 10^(-11) m`

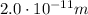
The energy of these photons is 2.5 times greater, so

`E=(2.5)(4\cdot 10^(-15) J)=1\cdot 10^(-14) J`

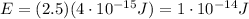
And by applying the same formula used at point 1, we find the corresponding wavelength:

`\lambda=((6.63\cdot 10^(-34)Js)(3\cdot 10^8 m/s))/(1\cdot 10^(-14) J)=2.0\cdot 10^(-11)m`