Answer:
The correct option is d.
Explanation:
It the given table,
A : Plate is a strike.
B : Plate is a ball.
C : Pitch over the plate.
D : Pitch not over the plate.
Formula for conditional probability is
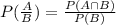
a) The probability that a pitch not over the plate is a strike is zero. So,
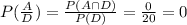
Therefore option 1 is accurately described or accurately calculated.
b) The probability that a pitch not over the plate is a ball is 1. So,
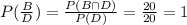
Therefore option 2 is accurately described or accurately calculated.
c) The probability that a pitch over the plate is a strike is 10:15. So,

Therefore option 3 is accurately described or accurately calculated.
d) The probability that a pitch over the plate is a ball is 5:10. So,
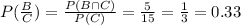
Therefore option 4 is inaccurately calculated.
Hence the correct option is d.