Question

what is the perimeter of the triangle shown on the coordinate plane. to the nearest tenth of a unit? 20.6 22.7 25.6 27.6​

Answer 1

25.6

Explanation:

Answer 2

Answer: 25.6 units

Explanation:

In the given picture , it can be seen that the triangle is passing through three points (-5,4) , (1,4) and (3, -4).

Using distance formula , we find the side -lengths of the triangle.

The distance between two points (a,b) and (c,d) is given by :_

`D=√((d-b)^2+(c-a)^2)`

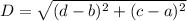
The distance between two points (-5,4) and (1,4):

`d_1=√((4-4)^2+(1-(-5))^2)=√(0+(6)^2)=6\ units`

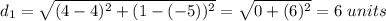
The distance between two points (1,4) and (3, -4).:

`d_2=√((-4-4)^2+(3-1)^2)\\\\=√((-8)^2+(2)^2)\\\\=√(64+4)=√(68)\approx8.25\ units`

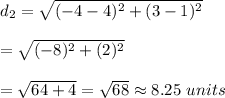
The distance between two points (-5,4) and (3, -4).:

`d_3=√((-4-4)^2+(3-(-5))^2)\\\\=√((-8)^2+(8)^2)\\\\=√(64+64)=√(128)\approx11.31\ units`

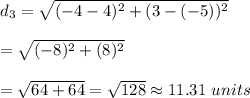
Now, the perimeter of triangle =
`d_1+d_2+d_3`

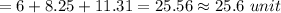`=6+8.25+11.31=25.56\approx25.6\ unit` ( to the nearest tenth of a unit)

Hence, the perimeter of the triangle shown on the coordinate plane. = 25.6 units