The function
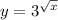 exhibits slow, continuous growth for
exhibits slow, continuous growth for
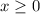 , approaching but never reaching a horizontal asymptote at y = 1. The y-intercept is at (0, 1).
, approaching but never reaching a horizontal asymptote at y = 1. The y-intercept is at (0, 1).
The given function is
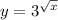 , where x is the exponent of 3 raised to the power of the square root of x. Let's analyze the behavior of this function:
, where x is the exponent of 3 raised to the power of the square root of x. Let's analyze the behavior of this function:
1. Domain: The function is defined for
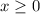 since the square root of any non-negative number is real.
since the square root of any non-negative number is real.
2. Vertical Asymptote: As x approaches negative infinity, the square root term approaches 0, and
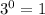 . Therefore, the function has a horizontal line at y = 1 as a vertical asymptote.
. Therefore, the function has a horizontal line at y = 1 as a vertical asymptote.
3. Growth: As x increases, the square root of x increases, and
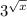 grows exponentially. However, the growth is slower than a standard exponential function due to the square root.
grows exponentially. However, the growth is slower than a standard exponential function due to the square root.
4. Y-Intercept: When x = 0, the function evaluates to
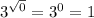 , so the y-intercept is at (0, 1).
, so the y-intercept is at (0, 1).
Given these characteristics, the graph should exhibit a slow but continuous growth, approaching but never reaching the horizontal line y = 1 as x decreases to negative infinity.
The probable question may be:
Explain the graph which represents y=3^ {square root x}.