Question

If the amplitude of a simple harmonic oscillator is doubled, what would happen to: (a) the period of oscillation, (b) the total energy, and (c) the maximum velocity of the mass oscillating?

Answer 1

(a) The period will not change

The period of oscillation of a simple harmonic oscillator is given by:

`T=2\pi \sqrt{(m)/(k)}`

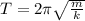
where

m is the mass

k is the spring constant

As we can see from the equation, the period of oscillation does not depend on the amplitude: therefore, if the amplitude of the oscillator is doubled, the period will not change.

(b) The total energy will quadruple

The total mechanical energy of a simple harmonic oscillator is given by

`E=(1)/(2)kA^2`

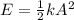
where this term represents the maximum elastic potential energy when the spring is completely compressed/stretched (so, when kinetic energy is zero), and where

k is the spring constant

A is the amplitude

In this problem, the amplitude is doubled:

A' = 2A

Therefore, the new total energy will be:

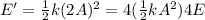`E'=(1)/(2)k(2A)^2=4((1)/(2)kA^2)4E` (1)

So, the total energy will quadruple.

(c) The maximum velocity will double

The maximum velocity of the mass oscillating is achieved when the mass crosses the equilibrium position: at that point, the elastic potential energy is zero (because the displacement is zero), and so the total energy is simply

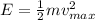`E=(1)/(2)mv_(max)^2` (2)

where

m is the mass

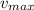`v_(max)` is the maximum velocity

Since the total energy must be conserved, then it must be

(1) = (2)

So we can write:

`(1)/(2)mv_(max)^2=(1)/(2)kA^2`

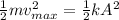
which can be rewritten as

`v_(max)= A \sqrt{(k)/(m)}`

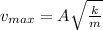
In this problem, the amplitude is doubled:

A' = 2A

Therefore, the new maximum velocity is

`v_(max)'= (2A) \sqrt{(k)/(m)}=2 v_(max)`

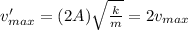
So, the maximum velocity will double.