Given :
There are currently 260 people in archery clubs across the city, and this number is increasing by 11% per year.
To Find :
An equation that can be used to find the number of people, y, in archery clubs across the city after 8 years.
Solution :
Increase in people after 1 years :
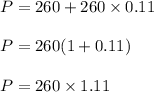
After 2 years :

Therefore, after 8 years the expression of population is :

Hence, this is the required solution.