Answer:
Check the attached graph
Explanation:
Given equation is
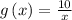 .
.
Now we need to graph the given equation
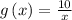 ..
..
Clearly it is not linear as equation is not of the form
 . So we need to find some points on given equation
. So we need to find some points on given equation
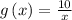 . by plugging some random values of x like -5,-3,1,... etc.
. by plugging some random values of x like -5,-3,1,... etc.
for x=-5, we get:
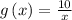
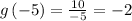 .
.
Hence first point is at (-5,-2). Similarly we can find more points and graph those points.
x can't be 0 as division by 0 is not defined so it will have vertical asymptote at x=0.
Since degree of numerator is less than degree of denominator so y=0 will be horizontal asymptote.
Now join those points by a curved line to get final graph.