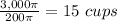Answer:
Part a)
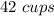
Part b)
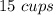
Step-by-step explanation:we know that
The volume of the sink (half sphere) is equal to
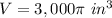
Part a) One cup has a diameter of 6 in. and a height of 8 in. How many cups of water must Michael scoop out of the sink with this cup to empty it?
The volume of the cylinder is equal to
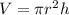
we have
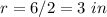 ----> the radius is half the diameter
----> the radius is half the diameter
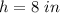
substitute the values
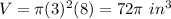
To find the number of cups divide the total volume of the sink by the volume of the cylinder
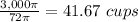
Round to the nearest whole number
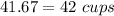
Part b) One cup has a diameter of 10 in. and a height of 8 in. How many cups of water must Michael scoop out of the sink with this cup to empty it?
The volume of the cylinder is equal to
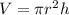
we have
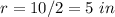 ----> the radius is half the diameter
----> the radius is half the diameter
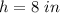
substitute the values
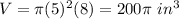
To find the number of cups divide the total volume of the sink by the volume of the cylinder