Answers:
The expression for the relativistic energy
 is given by:
is given by:
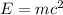 (1)
(1)
being
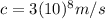
This famous equation includes the relativistic Kinetic energy
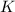 and the energy at rest
and the energy at rest
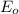 :
:
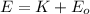 (2)
(2)
Where:
 (3)
(3)
Being
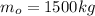 the mass at rest for the meteorite
the mass at rest for the meteorite
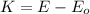 (4)
(4)
In addition, there is a relation between the relativistic energy and the momentum
 :
:
 (5)
(5)
Where:
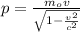 (6)
(6)
Knowing this, let's begin with the answers:
a)Momentum
In order to solve this part, equation (6) will be helpful, since we already know the mass of the meteorite and its speed
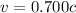 :
:
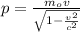
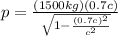
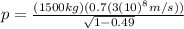
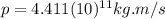 (7) >>>>This is the meteorite's momentum
(7) >>>>This is the meteorite's momentum
b) Total Energy
Remembering equation (5), which relates the total energy with the momentum:

We can substitute the value of the momentum found on (7):
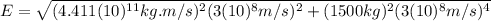
Then:
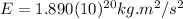
Knowing
 :
:
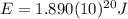 (8)>>>This is the total energy of the meteorite
(8)>>>This is the total energy of the meteorite
c) Energy at rest
Using equation (3):

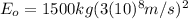
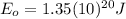 (9) >>>Meteorite's energy at rest
(9) >>>Meteorite's energy at rest
d) Relativistic kinetic energy
According to equation (4) the relativistic kinetic energy depends on the total energy and the energy at rest:
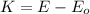
We already know the values of
 and
and
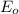 from (8) and (9). Hence we only have to substitute them on the equation:
from (8) and (9). Hence we only have to substitute them on the equation:
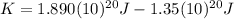
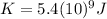 >>>Meteorite's Relativistic energy
>>>Meteorite's Relativistic energy