Question

10 students are standing equidistant from the center of a classroom. they are all holding hands to begin with. they must go and shake hands with all other students whose hands they are not holding. no handshake will occur more than once. how many handshakes will take place? ​

Answer 1

35

Explanation:

i dont know how to explain how i got the anwser

Answer 2

45 handshakes will take place in total in the party

Explanation:

Total number of students who attended the party = 10

Number of students needed to make one handshake = 2

Given that : no handshake will occur more than once.

⇒ No repetition of handshakes will be there.\

We need to find the total number of handshakes that took place in the party

`\implies\text{Total number of handshakes = }_2^(10)\txterm{C}`

`\implies\text{Total number of handshakes = }(10!)/(2!* 8!)`

`\implies\text{Total number of handshakes = }(10* 9)/(2)`

`\implies\text{Total number of handshakes = }45`

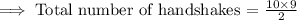
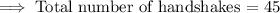
Therefore, 45 handshakes will take place in total in the party