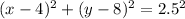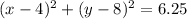Answer:
Center: (4,8)
Radius: 2.5
Equation:
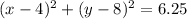
Explanation:
It was given that; the endpoints of the longest chord on a circle are (4, 5.5) and (4, 10.5).
Note that the longest chord is the diameter;
The midpoint of the ends of the diameter gives us the center;
Use the midpoint formula;
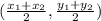
The center is at;
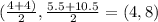
To find the radius, use the distance formula to find the distance from the center to one of the endpoints.
The distance formula is;
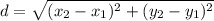
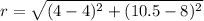
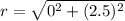
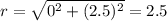
The equation of the circle in standard form is given by;
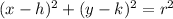
We substitute the center and the radius into the formula to get;