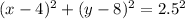Question

Select the correct answer from each drop-down menu.

The endpoints of the longest chord on a circle are (4, 5.5) and (4, 10.5).
The center of the circle is at the point ___ , and its radius is___ units. The equation of this circle in standard form is ___.

Options for first blank- (-4, 6.75), (4,8), (4, 9.25), (4, 16)
Options for second blank- 1.25, 2.5, 3.75, 6.25
Options for third blank- (x-4)^2+(y-8)^2=2.5,
(x+4)^2+(y+8)^2=2.5,
(x-4)^2+(y-8)^2=6.25
(x+4)^2+(y+8)^2=6.25

Answer 1

Answer and Step-by-step explanation:

The longest chord on the circle is the diameter, and the center of the circle is the midpoint of the diameter.

Use the midpoint formula to find the center

the x-coordinates are the same, so you can just subtract the y-coordinates to find the radius.

10.5 - 8 = 2.5

The equation of the circle is (x - h)² + (y - k)² = r² where r is the radius and (h, k) is the center.

(x - 4)² + (y - 8)² = 6.25

Answer 2

Center: (4,8)

Radius: 2.5

Equation:
`(x-4)^2+(y-8)^2=6.25`

Explanation:

It was given that; the endpoints of the longest chord on a circle are (4, 5.5) and (4, 10.5).

Note that the longest chord is the diameter;

The midpoint of the ends of the diameter gives us the center;

Use the midpoint formula;

`((x_1+x_2)/(2),(y_1+y_2)/(2) )`

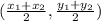
The center is at;
`((4+4))/(2) ,(5.5+10.5)/(2)=(4,8)`

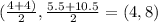
To find the radius, use the distance formula to find the distance from the center to one of the endpoints.

The distance formula is;

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`r=√((4-4)^2+(10.5-8)^2)`

`r=√(0^2+(2.5)^2)`

`r=√(0^2+(2.5)^2)=2.5`

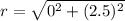
The equation of the circle in standard form is given by;

`(x-h)^2+(y-k)^2=r^2`

We substitute the center and the radius into the formula to get;

`(x-4)^2+(y-8)^2=2.5^2`

`(x-4)^2+(y-8)^2=6.25`