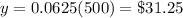Question

the interest earned on an account varies directly with the balance in the account. if an account with a balance of $200 earns $12.50 in interest, find the amount of interest earned on an account with a balance of $500

Answer 1

`\$31.25`

Explanation:

A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
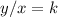`y/x=k` or
`y=kx`

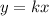
Let

y-------> the interest earned on an account

x------> the balance in the account

step 1

Find the constant k of proportionality

For
`x=\$200,y=\$12.50`

`k=y/x`

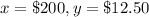
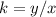
substitute the values

`k=12.50/200=0.0625`

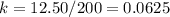
The equation is

`y=0.0625x`

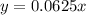
step 2

Find the amount of interest earned on an account with a balance of $500

so

For
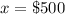`x=\$500` substitute in the equation and solve for y

`y=0.0625(500)=\$31.25`