Question

18. Find m∠D if m∠A = 2x + 18 and m∠B = 9x – 14.

A. 73°
B. 50°
C. 130°
D. 107°

Answer 1

Answer: The correct option is (C) 130°.

Step-by-step explanation: We are given to find the measure of ∠D from the figure, where

`m\angle A=2x+18,~~~\textup{and}~~~m\angle B=9x-14.`

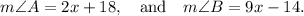
From the figure, we note that ABCD is a parallelogram.

So, AD is parallel to BC and AB acts as a transversal.

Then, the sum of the measures of angles A and B is equal to 180°, since they are interior angles on the same side of the transversal.

That is,

`m\angle A+m\angle B=180\\\\\Rightarrow 2x+18+9x-14=180\\\\\Rightarrow 11x+4=180\\\\\Rightarrow 11x=180-4\\\\\Rightarrow 11x=176\\\\\Rightarrow x=(176)/(11)\\\\\Rightarrow x=16.`

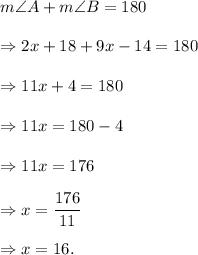
So, the measure of angle B is

`m\angle B=9x-14=9* 16-14=144-14=130^\circ.`

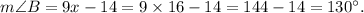
We know that the measures of the opposite angles of a parallelogram is 130°, so

the measure of angle D is 130°.

Thus, m∠D = 130°.

Option (C) is CORRECT.