Question

Step by step on how to solve this problem?

Answer 1

x =
`(3)/(2)`

Explanation:

Given the graph intersects the y- axis at (0, - 18), then substitute the coordinates into the equation y = x² + bx + c

- 18 = 0 + 0 + c ⇒ c = - 18

In the same way substitute (6, 0) into the equation

0 = 6² + 6b - 18

0 = 36 + 6b - 18

0 = 18 + 6b ( subtract 18 from both sides )

- 18 = 6b ( divide both sides by 6 )

- 3 = b

Hence equation is

y = x² - 3x - 18

Given the equation in standard form : y = ax² + bx + c : a ≠ 0

Then the x- coordinate of the vertex is

`x_(vertex)` = -
`(b)/(2a)`

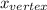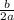
y = x² - 3x - 18 is in standard form

with a = 1, b = - 3, c = - 18, hence

`x_(vertex)` = -
`(-3)/(2)` =
`(3)/(2)`

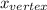The x- coordinate of the turning point is
`(3)/(2)`