Question

Question 4 (1 point)

A ball is thrown from a mountain 960 feet high, into the air with an upward velocity of 64 ft/s. When did the ball hit the

ground? And What was the max height it reached?

Answer 1

The ball will hit the ground at 10 seconds and its maximum height is 1024 feet.

Explanation:

Height of a mountain, h = 90 feet

Upward velocity of a ball, u = 64 ft/s

Its height as a function of time can be written by using the second equation of motion as follows :

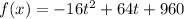`f(x) = -16t^2 + 64t + 960` .....(1)

When it will hit the ground, f(x) = 0

`-16t^2 + 64t + 960=0\\\\16(-t^2+4t+60)=0\\\\-t^2+4t+60=0`

It is quadratic equation.

t = -6 s and t = 10 s

Neglecting -6 seconds, the ball will hit the ground at 10 seconds.

For maximum height,

Put f'(x) = 0

`-32t+64=0\\\\\\t=(64)/(32)\\\\t=2\ s`

Put t = 2 in equation (1)

`f(2) = -16(2)^2 + 64(2) + 960\\\\=1024\ \text{feet}`

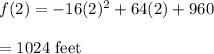
Hence, the ball will hit the ground at 10 seconds and its maximum height is 1024 feet.