Answer:
Part a) The approximate years were 1998 and 2008
Part b) The graph in the attached figure
Explanation:
Part a) we have
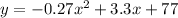
For
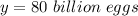
Solve the quadratic equation
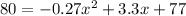

we know that
The formula to solve a quadratic equation of the form
 is equal to
is equal to

in this problem we have

so
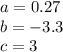
substitute in the formula
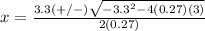
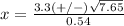
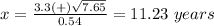

therefore
The approximate years are
1997+11=2008
1997+1=1998
Part b)
Using a graphing tool
we have
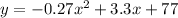
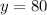
The solution of the system of equations is the intersection point both graphs
The intersection point are (0.99,80) and (11.23,80)
see the attached figure
therefore
The solution part a) is correct