Answer:
The quadratic equation has two complex solutions
Explanation:
we know that
The formula to solve a quadratic equation of the form
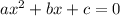 is equal to
is equal to
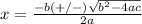
in this problem we have
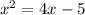
Equate to cero
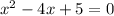
so
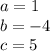
substitute in the formula
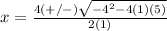
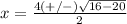
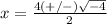
Remember that
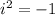
so
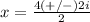
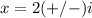
therefore
The quadratic equation has two complex solutions