Question

The engineer designed the valve such that it would produce a mean pressure of 5.0 pounds/square inch. It is believed that the valve performs above the specifications. The valve was tested on 6 engines and the mean pressure was 5.4 pounds/square inch with a standard deviation of 0.7. A level of significance of 0.025 will be used. Assume the population distribution is approximately normal. Make the decision to reject or fail to reject the null hypothesis.

Answer 1

The calculated value t = 1.399 < 2.5705 at 0.025 level of significance

Null hypothesis is accepted

The population distribution is approximately normal

Explanation:

Step(i):-

Given mean of the Population = 5.0

sample size 'n'= 6

The mean of the sample x=5.4 pounds /square inch

The standard deviation of the sample (S) = 0.7

Level of significance = 0.025

Null Hypothesis : The sample came from population

H₀ : x⁻ = μ

Alternative Hypothesis :H₁ : x⁻ ≠ μ

Step(ii):-

Test statistic

`t = (x^(-) -mean)/((S)/(√(n) ) )`

`t = (5.4 -5.0)/((0.7)/(√(6) ) )`

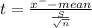
t = 1.399

Degrees of freedom = n-1 =6-1 =5

The tabulated value

t = 2.5705

The calculated value t = 1.399 < 2.5705 at 0.025 level of significance

Null hypothesis is accepted

The population distribution is approximately normal