Question

Select all possible values for x in the equation x^3=375?

Answer 1

Hello!

The answers are:

The possible values for x in the equation, are:

First option,
`5\sqrt[3]{3}`

Second option,
`\sqrt[3]{375}`

Why?

To solve the problem, we need to remember the following properties of the exponents and roots:

`a\sqrt[n]{b}=\sqrt[n]{a^(n)*b} \\\\\sqrt[n]{a^(m) }=a^{(m)/(n)}\\\\(a^(b))^(c)=a^(b*c)`

Then, we are given the expression:

`x^(3)=375`

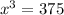
So, finding "x", we have:

`x^(3)=375\\\\(x^(3))^{(1)/(3) } =(375)^{(1)/(3)}\\\\x=\sqrt[3]{375}=\sqrt[3]{125*3}=\sqrt[3]{125}*\sqrt[3]{3}=5\sqrt[3]{3}`

Hence, the possible values for x in the equation, are:

First option,
`5\sqrt[3]{3}`

Second option,
`\sqrt[3]{375}`

Have a nice day!